二次方程式の解き方の1つに、「平方根を利用した解き方」があります。
なんだか難しそうですが、けっしてそんなことはありません。
中学生で学んできた知識をひとつひとつ順番に丁寧に積み上げていけば、平方根を利用した二次方程式は簡単に解くことができます。
「数学が苦手」
「中学の途中でついていけなくなっちゃった」
そんなあなたにも、無理なく理解できるようにまとめています。
この記事を読んで、「平方根を利用した二次方程式解き方」を一緒にマスターしちゃいましょう!
二次方程式とは?
二次方程式とは、このような形をした式のことをいいます
![]()
二次方程式は
- 二次・・・Xの右上についている数字の中で一番大きい数が「2」であるということ。

- 方程式・・・式をいじることによって、最終的に(左辺)=0の形にできる式のこと。
を表しています。
ですから移行したり、展開することで、
![]()
の形にすることができる、以下の式も二次方程式なのです。
![]()
![]()
平方根を使って二次方程式を解く
平方根を使って二次方程式を解くためには、二次方程式を、次の形にすることが必要です。
![]()
(Xを含んだ式)の二乗=ただの数字
次は、この左辺の2乗を外してみましょう。
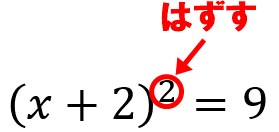
二乗の外し方
2乗の外し方を、もっと簡単な例で考えてみましょう。
![]()
この3の二乗から、右上に書いてある2乗の部分を取りたいとします。

その時は、√(ルート)を上からかぶせます。

そして、ルートと、2をセットで取り除きます。
ただし、ルートと、2を取り除いた後は、必ず±もつけましょう。

二次方程式で二乗を外す
二次方程式でもすることは全く同じです。
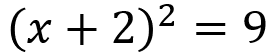
この式の両辺に√(ルート)を付けます。
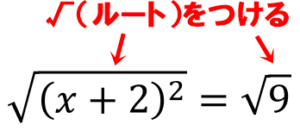
右辺の9は3の二乗に変更できるので、その形にします。
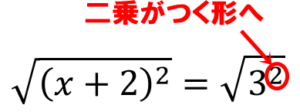
最後にルートと二乗を両方とってしまいましょう。
そのあと、±をつけることも忘れずに!

次にX=の形にするために、左辺の2を、右辺に移項させましょう。
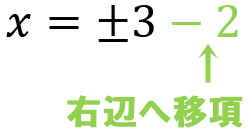
上の式はX=3-2、X=-3+2の2つの式が合体した式です。
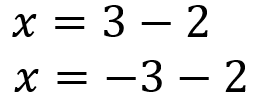
それぞれを計算して、最終的な、答えX=1、X=-1が導き出されます。
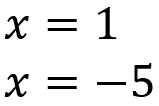
これで、平方根を用いた二次方程式の解き方です。
内容を参考に練習問題をたくさん解いて、平方根を用いた二次方程式の解き方をマスターしてくださいね!